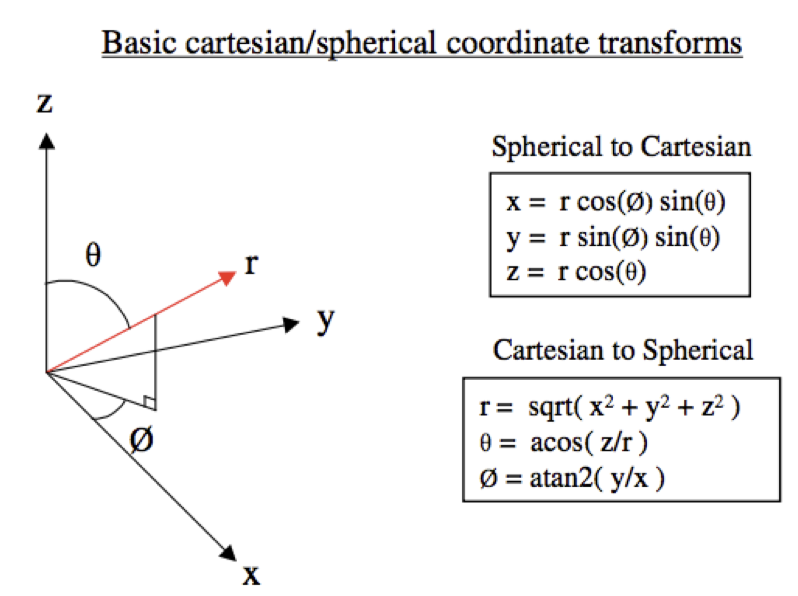
As mentioned in my intro post, the individual antennas in an array are often known as “elements”. To compute the arrays performance each individual elements field contribution needs to be summed. For my initial investigation I focus on using a rectangular microstrip patch element and this post will cover the model that is used.
A microstrip or patch antenna is a low profile antenna that has a number of advantages over other antennas – it is lightweight, inexpensive, and easy to integrate with accompanying electronics because they can be printed directly onto a circuit board which makes them easy to fabricate.
A patch antenna usually consists of a conductive patch with width W, and length L, sitting on top of a substrate (i.e. a dielectric circuit board) with thickness h and relative permittivity Er. The substrate then sits on top of a conductive ground plane.
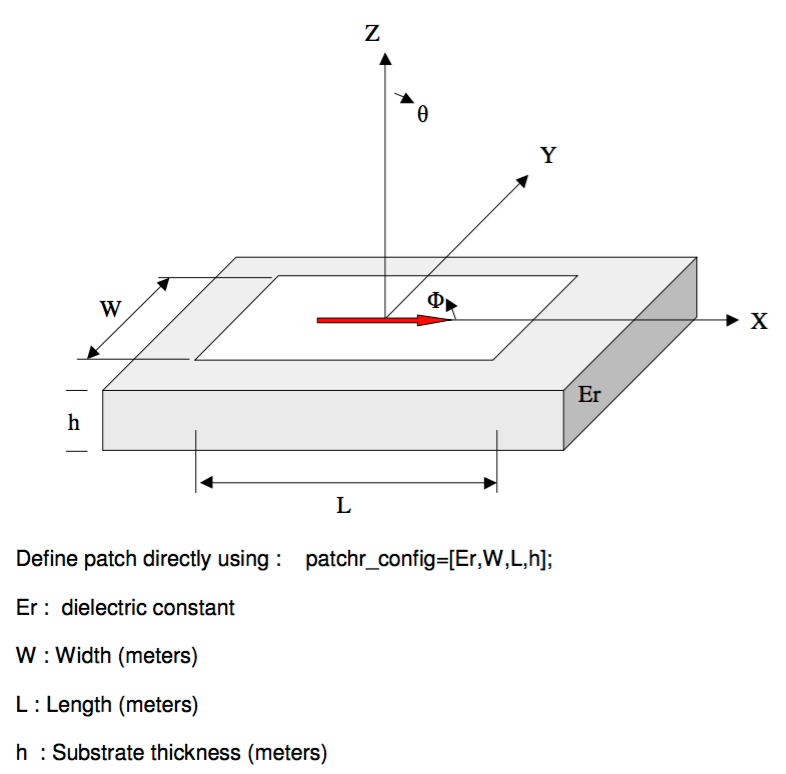
With the model used there is no account taken of mutual coupling between the elements. This can have a significant effect on array performance when array elements themselves are large, elements are closely spaced or large scan angles are used. It is also assumed the ground plane is infinite so the model is only valid over 0°<theta<90°, 0°<phi < 360°. The benefits of this model are the calculation is potentially very fast and despite the limitations the model still provides enough accuracy to give a useful insight into the potential performance of an array, before committing to more detailed modelling or prototyping.
The E theta and E phi components of the far-field radiation pattern are given by the equations below:
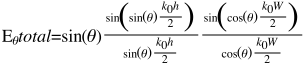
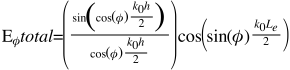
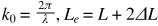
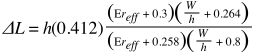
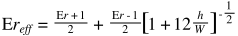
Using these equations allows us to create the following Python function to calculate the total E-field pattern for the patch as a function of theta and phi:
Before moving on to the array calculation itself next time I’ll detail the Python scripts I use to visualise the fields as it’s always nice to see what’s going on.