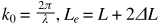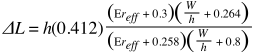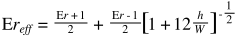Technology | The Geeky Grower

Scotcoin

Earlier this week I attended the Scotcoin & the blockchain meetup at Napier University. It was a Q&A session, there must have been around 25 people there and it was an informative and interesting evening.

The two Scotcoin representatives were approachable and enthusiastic and seemed genuinely pleased to host the meetup and field the questions. The attendees were a mixed bag of crypto geeks, anti-establishmenters and nationalists. Some with pretty passionate opinions they weren’t scared to show. It led to a pretty entertaining interaction. In a way I think the mix of people reflected the mixed Scotcoin vision.

Scotcoin was initially conceived during the build up to the 2014 Scottish Independence Referendum. At this time it was unclear what the currency situation would be if Scotland went independent and Scotcoin was a potential solution. As an ambitious, alternative solution to the currency issue I think it was quite smart (although I doubt the Scottish Government would have had the vision or courage to implement it).

However, Scotland didn’t become independent…The original Scotcoin founder left the project and a new investor/team took over. At that point I think it became less an idealistic vision and more like a way for some people to make money. -which is fair enough.

Nevertheless, according to the Business Model Canvas, a successful product must:

“Provide value to the customer by resulting in the solution of a problem the customer is facing or providing value to the customer.”

Without the need for an alternative to the GBP Scotcoin no longer seems to meet these requirements.

The official project line was that “Scotcoin will grow the Scottish economy by offering small business owners benefits.” When questioned on what those benefits are the only one suggested was lower transaction fees – a benefit that more established cryptocurrencies like Bitcoin (which Scotcoin is basically modelled on) already provide.

There was mention of the development of other features, but these couldn’t be discussed and I struggle to see the team having enough talent or vision to truly innovate. Whilst I hope the project doesn’t fail, for now, like a lot of crypto projects out there I think it’s mainly fueled on pure speculation.

Antenna Arrays And Python – The Array (finally!)

As mentioned in my intro post an array antenna is a set of individual antennas connected to work as a single antenna. So far we’ve covered the individual antennas, i.e. the square patches, now it’s time to look at how they can be connected to work together.

Array Factor Fun

You can’t get far digging into arrays before you come across the Array Factor. It looks complicated but to me the easiest way to think of it is that it combines every elements position, radiating amplitude and radiating phase to give the overall array performance.

The Array Factor demonstrates that by altering an element, such as its position or phase, we can alter the arrays properties. For example the arrays beam could be steered to a desired position by altering the phase of each element.

The Array Factor is given by:

Where:

θ, φ = Direction from origin

N = number of elements

An= Amp of element

βn = Phase of element in rads

k0 = 2π/λ rads/m

And:

is the relative phase of incident wave at element n located at xn, yn, zn.

Array Factor in Python

The script below shows how easy it is to calculate the Array Factor in Python:

Array Radiation Pattern, Directivity & Gain

The above Array Factor equation is independent of each elements individual radiating pattern. The overall radiation pattern of an array is determined by the array factor combined with the radiation pattern of each element, Fn(θn, φn), giving:

The overall radiation pattern results in a certain directivity and thus gain linked through the efficiency as discussed previously.

Some Examples

To demonstrate the effects the individual element patterns have on the overall array performance we can investigate some examples using Python.

Isotropic antenna elements

In this case each element radiates equally in all directions so Fn(θn, φn) is the same for each θn, φn. The antenna radiation pattern is now just the Array Factor as described in the code above.

Patch antenna elements

Using elements described by the PatchFunction discussed previously:

PatchFunction(θ, φ, Freq, 10.7e-3, 10.47e-3, 3e-3, 2.5)

Python script for patch array:

Horn antenna elements

And finally using horn antenna elements represented by cos²⁸(θ) function.

Python script for horn array:

Next time we can see how to calculate an elements phase to steer the beam.

Antenna Arrays And Python – Patch Efficiency & Gain

Last post I dealt with antenna directivity, this post discusses antenna gain which is closely related.

Gain combines an antennas directivity and efficiency to describe how good it is at sending/receiving power in a direction. This is useful for things like link budget analysis which basically calculates if two antennas can communicate.

Antenna Gain, G, can be calculate from the directivity, D, and antenna efficiency, εr by:

The efficiency of an antenna describes how well the input power is radiated by the antenna (and due to reciprocity receive efficiency is the same as transmit efficiency):

A high efficiency antenna will radiate most of the input power while a low efficiency antenna will lose a lot of the input power before it is radiated due to things like dielectric loss, impedance mismatch, etc.

Patch Efficiency

The Python script at the bottom of the post is based on the ArrayCalc calc_patchr_eff.m file and defines a function, CalculatePatchEff, that calculate the efficiency of a rectangular patch based on the patch dimensions and materials. The comments provide some example material properties and the main function has some examples that demonstrate the effects of the material selection on the efficiency:

FR4 Patch, 14GHz, Efficiency = 47.27%

RO4350 Patch, 14GHz, Efficiency = 62.32%

Python Script

Antenna Arrays And Python – Calculating Directivity

Directivity is a measure of how directional an antenna’s radiation pattern is. For example an antenna that radiates strongly in one direction has a high directivity while an antenna that radiates equally in all directions has a low directivity.

It is not necessarily a bad thing to have an antenna with low directivity, it depends on the application. For example:

To communicate with a geosynchronous satellite 35,786km away we need an antenna that produces a strong beam directed towards the satellite. In this case a parabolic dish antenna is often used because it has a high directivity.

Alternatively a mobile phone needs to be able to connect to a cell tower no matter what orientation the phone is held which means no matter what direction it’s antenna is pointing. In this case an antenna with a low directivity is used so that the antenna can receive/transmit well in any direction.

Calculating Directivity

Directivity can be calculated using the equation below which basically means the max value of radiated power divided by the average power in all directions:

Where:

Directivity is often expressed in dBi and represents the dB ratio with respect to an isotropic radiator.

Python Script – Directivity.py

The gist below shows my Python script for calculating the directivity (based on the ArrayCalc calc_directivity.m file).

The main function is:

CalcDirectivity(Efficiency, RadPatternFunction, *args)

This takes a function argument, RadPatternFunction, as an input. This function should describe the antennas radiation pattern in terms of theta and phi.

At the bottom of the script there are some basic examples showing how to calculate the directivity for three different radiation patterns – an isotropic antenna and two sin functions. Below this there are also two examples calculating the directivity for rectangular patches using the functions discussed in my Square Patch Element post.

The efficiency argument to RadPatternFunction is related to the Gain of the antenna and will be discussed in my next post.

Antenna Arrays And Python – Square Patch Element

As mentioned in my intro post, the individual antennas in an array are often known as “elements”. To compute the arrays performance each individual elements field contribution needs to be summed. For my initial investigation I focus on using a rectangular microstrip patch element and this post will cover the model that is used.

A microstrip or patch antenna is a low profile antenna that has a number of advantages over other antennas – it is lightweight, inexpensive, and easy to integrate with accompanying electronics because they can be printed directly onto a circuit board which makes them easy to fabricate.

A patch antenna usually consists of a conductive patch with width W, and length L, sitting on top of a substrate (i.e. a dielectric circuit board) with thickness h and relative permittivity Er. The substrate then sits on top of a conductive ground plane.

With the model used there is no account taken of mutual coupling between the elements. This can have a significant effect on array performance when array elements themselves are large, elements are closely spaced or large scan angles are used. It is also assumed the ground plane is infinite so the model is only valid over 0°<theta<90°, 0°<phi < 360°. The benefits of this model are the calculation is potentially very fast and despite the limitations the model still provides enough accuracy to give a useful insight into the potential performance of an array, before committing to more detailed modelling or prototyping.

The E theta and E phi components of the far-field radiation pattern are given by the equations below:

Using these equations allows us to create the following Python function to calculate the total E-field pattern for the patch as a function of theta and phi:

Before moving on to the array calculation itself next time I’ll detail the Python scripts I use to visualise the fields as it’s always nice to see what’s going on.

Blockchains & Digital Currency

Warning, this is a bit of a brain spew!

Digital currency such as Bitcoin and Ethereum and the blockchains they are built on are exciting and interesting technologies. I’ve been following various blogs about them for some time and there are often comparrisons to the early days of the internet. If that’s the case I want to be involved! But I’m not sure of the best way. And is it going to live up to the hype?

There appear to be two obvious ways to get into it. Firstly develop using the technologies or secondly – speculate on the associated currencies/tokens. I don’t know if I have the creativity or the time to dive into the development side of things although I do find it interesting, especially Ethereum. Speculating on the currency is easy enough to do, just purchase some, but it’s really just guess work, think I need to come up with some kind of strategy.